Are All Aspheric Contact Lenses Created Equal?
Aspheric contact lenses are underutilized, probably because they're not well understood. Using corneal topography, this report will help familiarize you with the various designs.
BY KENNETH A. LEBOW, OD
FEBRUARY 1999
Aspheric base curve contact lenses have been promoted as a means to improve the base curve-to-cornea fitting relationship in RGP designs and to correct presbyopia. Yet their usage in the United States has never been significant compared to traditional spherical base curve contact lenses. Reasons for this include practitioner unfamiliarity, difficulty confirming the accuracy of the base curve and its asphericity, questionable reproducibility and increased cost. Moreover, polishing aspheric base curve contact lenses can potentially change the curvature that was originally cut on the posterior lens surface.
Eccentricity and Shape
Spherical base curve lenses have a constant radius of curvature across the optic zone of the lens, while aspheric lenses have a changing radius of curvature across the optic zone of the lens. The rate of change in the base curve radius measured from the central apical radius to the periphery is defined as eccentricity. This is a mathematical term that describes the flattening of curvature for various geometric shapes. For example, a circle has no change in its radius and has an eccentricity of zero. Various shapes of ellipses are generated when the eccentricity of a sphere falls between zero and one. A parabola is defined by an eccentricity that equals one, and variously shaped hyperbolas are defined when the eccentricity exceeds one (Fig. 1).

FIG. 1: A comparison of various conicoids.
Shape factor is another term used to describe the flattening of a curved surface. It is similar to the eccentricity, but can mathematically represent both prolate (flattening) and oblate (steepening) surfaces. The relationship between shape factor and eccentricity is approximately expressed by the equation: SF = ecc2. Since the corneal surface can be described as an asymmetrical toroidal asphere, it seems logical that an aspheric contact lens surface matching the corneal asphericity could provide an ideal fitting relationship and improve on-eye comfort and patient adaptation.
While manufacturers go to great lengths to standardize aspheric lens designs, there are several ways to generate aspheric lens surfaces. Some manufacturers generate conicoid surfaces that mathematically resemble ellipses, while others use a series of spherical base curve zones to simulate a mathematical model of an ellipse. Regardless, each of these designs creates a contact lens base curve that flattens from its central apex to the periphery. As a result of this flattening factor, aspheric lenses are generally fit steeper than their spherical counterparts. The sagittal depth of the contact lens decreases as the eccentricity increases, so the central apical radius must be fit progressively steeper to achieve proper alignment of the lens on the eye (Fig. 2).
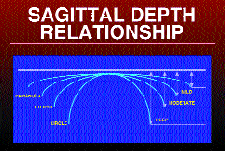
FIG. 2: As the eccentricity of the contact lens increases, its sagittal
depth decreases.
Measuring Up
You can use a traditional radiuscope to measure the central apical radius of an aspheric contact lens like you would with spherical lenses, but it may be more difficult to achieve a sharp clear image as the eccentricity increases. Sophisticated Moir� fringe devices are required to measure peripheral radius values and confirm the eccentricity of a lens. Hence, practitioners rely on the eccentricity and fitting suggestions stated by the manufacturers for these designs.
This paper is designed to show that a corneal topographer can be used to measure the base curve of spherical and aspheric contact lenses and present a global representation of their topographic characteristics. In gathering data for the following examples, multiple series of measurements were not obtained and only minimal efforts were made to ensure exact centration and avoid lens tilt. This paper doesn't represent the specific accuracy of base curve or eccentricity measurements between measured values and those claimed by the manufacturer. Rather, it shows unique curvature patterns consistent with true conic shapes as well as multiple spherical zones representing aspheric shapes.
A lens holder that was modified and adapted to the Humphrey Atlas Corneal Topography System enabled image capture using standard procedures for the corneal surface. After calibrating the topographer, a series of various spherical and aspheric contact lens designs with known base curves confirmed by radiuscope measurement were mapped and displayed using the overview display showing axial, tangential, elevation and profile maps of the concave lens surface measured topographically. General lens centration, topographer alignment and proper focusing were achieved in the same manor as instrument calibration. The Atlas topographer was chosen because its normalized or autoscale can detect curvature changes as small as 0.25D and because it numerically presents the shape factor of the measured surface, according to the manufacturer.
Single-Vision Designs
Figure 3 shows an overview display representing the base curve surface of a spherical lens (Lens #1). This map calculates curvature using the axial or sagittal radius assumption. The uniform green appearance across the base curve of the lens shows a relatively constant radius of curvature. The central radius of curvature was measured as 7.46mm for a 7.50mm radius base curve, but some variability in measurement across the lens surface is apparent. The shape factor is 0.01, indicating an essentially spherical curvature.
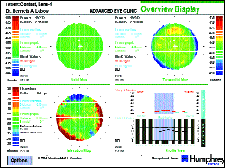
FIG. 3: Lens #1.32 |
.
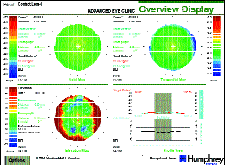
FIG. 4: Lens #2 |
Figure 4 shows an overview display of an aspheric base curve contact lens currently offered as an improved fitting design for non-presbyopic applications (Lens #2). The central apical radius of curvature measured 7.51mm for a confirmed 7.50mm requested base curve. Clearly evident are three zones of spherical curvature. The central zone, approximately 2.5mm in diameter, has a relatively constant radius that varies between 7.50 and 7.53mm. Surrounding this central zone is a 1.5mm ring of almost exactly 7.55mm radius, followed by a final peripheral zone measuring a relatively consistent 7.60mm radius. This lens design is labeled aspheric, but appears to be manufactured with three approximately concentric spherical zones. Its shape factor is 0.09, indicating a slight departure from circularity with only a very minor peripheral flattening.
Figure 5 shows an overview display of another aspheric base curve contact lens currently offered as an improved fitting design for non-presbyopic applications (Lens #3). The central apical radius measures 7.48 mm for a lens that was manufactured to be 7.50mm. However, the topography pattern appears uniquely different than the lens described in Figure 4. There is a central zone of relatively steep curvature that flattens from 7.48mm in the center to approximately 7.60mm within the first 1.5mm zone. Thereafter, the curvature continues flattening to an 8.23mm radius approximately 4mm from the center of the lens. The shape factor of this lens was 0.58, indicating a significant departure from circularity in spite of its non-presbyopic application.

FIG. 5: Lens #3.
In each of these examples, the central apical radius calculated by the topographer was very close to that measured by the radiuscope. Yet, the curvature patterns were different, so we'd expect the fitting relationship for each of the lenses to also be different.
Multifocals
Aspheric multifocal designs are similar to their single-vision counterparts, but exhibit much greater peripheral flattening factors (i.e., larger eccentricity or shape factor). Excessive peripheral flattening of the base curve produces a much shallower sagittal depth and requires a significantly steeper base curve-to-cornea fitting relationship to achieve on-eye alignment. Base curve topography patterns should demonstrate a more rapid rate of peripheral flattening, which should be obvious when viewing the axial map. Also, aspheric base curves are actually composed of both sagittal and tangential radii of curvature. Coincidentally, the Atlas Corneal Topography System measures an instantaneous or tangential radius centrally and peripherally. Based on the algorithm used to calculate the tangential radius, it is possible to measure both the tangential and sagittal radius at various points along the base curve surface. This feature may allow practitioners to gain more knowledge about the add power effect of these contact lenses.
Figure 6 shows an overview display of an aspheric multifocal base curve demonstrating axial, tangential, elevation and profile maps (Lens #4). The axial map shows a central steep zone of approximately 2.5mm with a measured base curve of 7.29mm, and the tangential map shows a 2.0mm central zone of steepening with a base curve of 7.53mm. The labeled base curve is 7.34mm. The shape factor is 0.44, which is less than one of the single-vision lenses (Fig. 5). The Elevation Map demonstrating the best-fit reference sphere to the measured data is 43.2D or 7.81 mm. This value is significantly flatter than either the central sagittal or tangential radii. While the profile view shows a true conicoid shape to the flat and steep curvatures, they appear slightly out of phase, indicating the possibility that the contact lens was not properly centered.
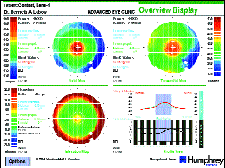
FIG. 6: Lens #4.
Figure 7 shows an overview display of another popular aspheric multifocal base curve demonstrating axial, tangential, elevation and profile maps (Lens #5). The axial map shows a 3.0mm zone, while the tangential map shows a 2.0mm zone of steep central curvature, measuring at the apex 7.41mm sagittally and 7.53mm tangentially. The labeled apical radius is 7.50mm. The surrounding zone of peripheral flattening demonstrates a shape factor of 0.71, indicating a greater rate of flattening than the previous lens design. The reference sphere measured 42.7D or 7.91 mm. The profile display shows a symmetrical conicoid profile, implying that the measurement was taken over a well-centered lens.

FIG. 7: Lens #5.
Figure 8 shows an overview display of another popular aspheric multifocal base curve demonstrating axial, tangential, elevation and profile maps (Lens #6). The steep central curvature zone measures approximately 2.0 mm on both the axial map and tangential maps, with the apical sagittal and tangential radii measured at 7.39mm and 7.33mm respectively. The similarity of these two measurements implies a multispherical curvature rather than a true aspheric curvature. The labeled apical radius is 7.55mm. A shape factor of 0.93 represents the greatest rate of peripheral flattening of all measured lenses and the reference sphere was 43.2D or 7.81mm. The profile display shows an arcuate pattern, again indicating the possibility that this lens may be manufactured with a series of concentric spherical zones.
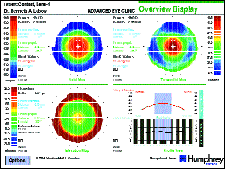
FIG. 8: Lens #6.
Table I compares a series of parameters for all the lenses measured and separates them into single-vision and multifocal designs. The #1 and #2 lenses showed good correlation between labeled and measured base curve radii with extremely low shape factors, confirming the presumption that they are single-vision designs. Lens #3 was clearly a different design, showing a shape factor more consistent with aspheric multifocal designs and a slight difference between the sagittal and tangential radii. Two multifocal lenses (#5 and #6) had significantly higher shape factors, but #5 appeared to be a true asphere, while #6 showed more properties of a single-vision design (i.e., minimal difference between sagittal and tangential radii and an arcuate profile). The #4 contact lens had properties of a true asphere (large difference between sagittal and tangential radii and a conicoid profile), but with a low shape factor, could be considered for a single-vision or early presbyopic application. The presentation and analysis of these topography patterns is completely preliminary and requires extensive investigation and verification to understand all of the variables involved in the design of aspheric contact lenses. This report merely demonstrates that all aspheric base curve contact lenses apparently are not created equal.


He is also a paid consultant for Humphrey Systems and Biocompatibles Eyecare.
THE EYESSENTIALS
|



