CORRECTING ABERRATIONS

Correcting Aberrations with Contact Lenses

Part 2 of our look at the current and future realities of correcting aberrations with contact lenses.

By Pete S. Kollbaum, OD, PhD, FAAO, & Arthur Bradley, PhD

Dr. Kollbaum is a research associate at Indiana University. He can be reached at kollbaum@indiana.edu. Arthur Bradley is a professor of Optometry and Vision Science at Indiana University. He can be reached at bradley@indiana.edu.

In Part 1 of this two-part series we examined some of the theoretical challenges anticipated for correcting higher-order aberrations (HOAs) with contact lenses. In this article, we'll examine the current status of aberration-controlling contact lenses and consider the pros and cons associated with different strategies for correcting aberrations.

How It Works

One way to describe how we need to alter a contact lens to correct aberration is to think of refractive error in terms of optical path lengths (OPL). The OPL is the "optical distance" each ray of light must travel from one point (object) to another (retina).

Figure 1 graphically demonstrates the computation of the change in OPL produced by a uniform slab of material that has a different refractive index than the surrounding medium. In air, the OPL between points A and B is simply the physical distance between the two points multiplied by the refractive index that the two points are in (n=1). However, a uniform slab of material placed into this path will introduce a net change in OPL equal to the product of the physical thickness of the slab and the change in refractive index (delta n).

Figure 2a shows the wavefront aberration function for simple myopic defocus. Wherever the aberrated wavefront lags behind the reference plane wave (dashed line), we refer to that part of the wavefront as "retarded" and wherever the wavefront is in front of the reference, we refer to the wavefront as "advanced."

To correct for this aberration it's necessary to effectively slow the propagation of the wavefront in areas of the pupil where it is advanced, and speed up the propagation of the wavefront in areas where it's retarded. To accomplish this we can introduce a slab of index greater than 1 into the optical path. This slab must be physically thicker in the areas corresponding to the pupil locations where the wavefront was advanced (to slow down the propagation) and physically thinner in areas where the wavefront was retarded.

In an ideal correction, the resultant wavefront, after passing through this variable thickness slab, would be a flat, plane wave. In the case of myopic defocus, we can observe that the slab required to compensate for the myopic wavefront is a negative powered lens with a thinner center and thicker periphery. We could extend this same theory to apply to any type of aberration (such as vertical coma [Figure 2b]) or any combination of aberration.

In correcting aberrations with contact lenses, the slab in the previous example is the lens material. So, to correct aberrations with contact lenses, we introduce localized changes in lens thickness. Essentially, a contact lens must be thinner in areas where the eye it is correcting shows the greatest delays in wavefront and thickest where the eye's wavefront demonstrates its greatest advancement. This results in the ideal eye+lens goal of a uniform spherical wavefront that focuses on the retina as a single focal point. Several authors (Thibos, Cheng et al, 2003; Almeida and Garcia, 2005) have demonstrated how this simple concept would be possible with GP and soft contact lenses.

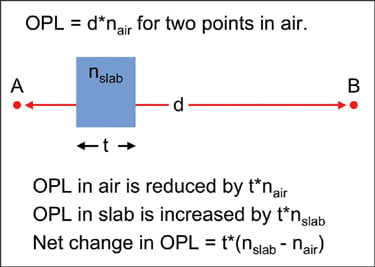
Figure 1. Schematic showing the optical path length change caused by a slab of higher refractive index material.

As an important part of the previous example (Figure 2), we begin to see the quantitative challenges involved in inducing aberration correction in a contact lens. For example, a contact lens aimed to correct –2.00D of defocus (over a 6mm pupil diameter) must be about 11.25 microns thicker at the lens periphery relative to the lens center, whereas a lens aimed to correct 0.1 microns of spherical aberration must have a relative thickness change of only approximately 0.25 microns.

Current Aberration-correcting Lens Designs

To date, we can group the two primary approaches adopted for aberration correction with contact lenses into two general categories: mass-produced lenses that aim to correct a fixed type and magnitude of aberration (correct for the mean aberration of the population); and custom lenses, which aim to correct the aberrations specific to an individual eye. Additionally, it's important to highlight that a lens could be designed to either correct only the corneal aberrations (based on corneal topography) or whole-eye aberrations (cornea plus internal optics).

Level of HOA and the Impact of Correction

The visual benefit of correcting higher-order monochromatic aberration varies among eyes (Guirao, Porter et al, 2002) and many, but not all, patients having eyes with normal vision will enjoy noticeable improvements from customized vision correction (Williams, Yoon et al, 2000). However, as we discussed in Part 1 of this series, there are issues that limit the benefit of correcting HOAs in normal eyes. Therefore, some investigators have focused on using contact lenses to correct eyes that remain highly aberrated following the correction of sphere and cylinder, such as keratoconic eyes (Thibos, 2000; de Brabander, Chateau et al, 2003; Sabesan, Jeong et al, 2007; Marsack et al, 2006; Marsack et al, 2007).

Keratoconic eyes reportedly have HOA levels as much as 5.5 times higher than those of normal eyes (Pantanelli, MaCrae et al, 2007) and thus, are expected to benefit the most from HOA correction. Custom soft lenses have been shown to provide a threefold reduction in aberration on keratoconic eyes (Sabesan, Jeong et al, 2007; Marsack et al, 2007) and improve acuity (de Brabander, Chateau et al, 2003), even in the presence of on-eye translations and rotations (See Part 1).

Commercially Available Aberration-correction Options

The aberration-correcting lenses used in the studies described above are not yet commercially available. However, there are commercially available aberration-correcting lenses in the marketplace today, with others reportedly coming in the near future. Here we'll discuss some representative designs currently in existence.

• Custom Lenses

WaveTouch lenses (WaveTouch Technologies, formerly Optical Connection) are custom designed soft lenses in which a whole-eye aberrometry measurement is taken of the naked eye in the clinician's office followed by another measurement taken of the eye wearing a predicate (blank) lens. This predicate lens blank is fiducially marked, prism-ballasted and of the exact same design as the lens which will have the aberration correction applied to it. This second aberrometry measurement determines the residual aberrations to correct, similar to an over-refraction. The clinician sends this information electronically to the manufacturer and, following a reported 48-hour production process, a lens is delivered to the clinician.

WaveTouch Technologies is working with several different aberrometer manufacturers so that practitioners could use different instruments to acquire the measurements. Currently, the approved instruments include the iTrace (Tracey Technologies) and 3D Wave Analyzer (Marco).

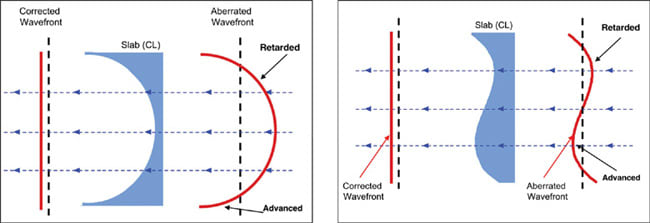
Figure 2. Schematic showing the correction of a (a) myopic and (b) comatic wavefront by the introduction of an aberration-correcting contact lens.

These lenses have been in development for the last several years, and WaveTouch Technologies is hopeful that they'll become available in the upcoming months.

The Wave custom lenses from EyeQuip employ a similar approach to the WaveTouch lenses, but with a quite different goal. The Wave custom lenses have specially lathed anterior and/or posterior surfaces designed to correct HOAs measured with the Keratron or Keratron Scout (Optikon) corneal topographers. Therefore, these lenses are designed to correct for corneal-only aberrations, which are different than whole-eye aberrations. For example, corneal spherical aberration is considerably greater than whole-eye spherical aberration.

The Wave lenses can be soft or GP and are available in sphere, toric, multifocal and orthokeratology designs. They're available with or without prism stabilization. With a lathed posterior surface to match the anterior cornea, there is potential for a relatively stable fit.

We ordered a Wave lens designed to correct for a moderately keratoconic subject. Figure 3a shows the Keratron axial topography of this moderately keratoconic eye. You can observe the typical inferior steepening. Figure 3b shows the anterior surface wavefront that the instrument used to fit this anterior corneal topography. Figure 3c shows the off-eye measured wavefront of the custom designed Wave soft lens manufactured to correct for these anterior corneal aberrations.

Based on the theory we previously described, we would anticipate portions of the lens designed to correct areas of high negative corneal aberration (shown in Figure 3b by the warmer, red colors) to have corresponding positive aberration (shown in Figure 3c by the cooler, blue colors).

We can observe that, based on the off-eye measurement of the lens, the lens design appears to fit the expectations with reasonable success. However, this may or may not be the case when we place this lens on the eye, due to the reasons we discussed in Part 1.

SynergEyes W (SynergEyes, Inc.) lenses are whole-eye wavefront-guided custom lenses currently in the very early stages of development. The SynergEyes lens is a high-oxygen-permeable hybrid lens with a GP lens center and soft skirt of 14.5mm overall diameter and 7.8mm optical zone diameter.

In addition to a lens design that corrects for simple ametropia (SynergEyes A), SynergEyes also makes a SynergEyes KC lens that has achieved good clinical success in keratoconus correction. The design intent and fitting strategy for the company's wavefront-corrected lenses is currently unknown, however. It's also uncertain when the SynergEyes W lenses will become available, but due to their size and design they have the potential to provide greatly increased on-eye stability compared to some other GP or soft lens designs. They may also have the potential for an improved optical correction due to their GP lens center.

• Population Mean Correcting Lenses

Due to the difficulties in implementing a large-scale manufacturing strategy of custom correcting lenses, several manufacturers have developed aspheric lenses to correct for the population average aberration level. However, this is not straightforward because the population average for most aberrations is 0 (Thibos 2002). The one exception to this is spherical aberration, for which the average eye, with a 6mm pupil, has approximately 0.12 microns of spherical aberration. Therefore, a lens designed to correct for the population mean HOA would include only a correction for spherical aberration (around –0.12 microns).

There are other reasons to target spherical aberration correction. First, standard spherical lenses have spherical aberration levels that vary with lens power (Dietze and Cox 2003; Kollbaum and Bradley 2005), with negative lenses exhibiting negative spherical aberration and positive lenses exhibiting positive spherical aberration. One additional advantage of a spherical aberration-correcting lens is that it would be insensitive to rotation on the eye, unlike a toric lens.

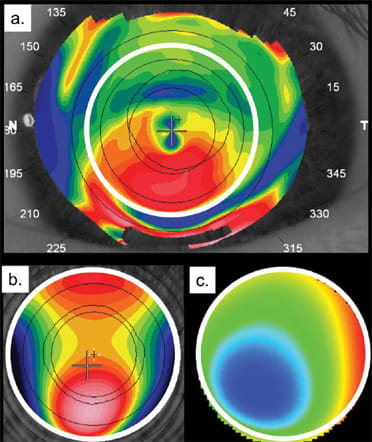
Figure 3. (a) The anterior axial corneal topography of a moderately keratoconic eye. (b) The anterior corneal wavefront obtained from the anterior surface topography of this eye. (c) The wavefront of the lens manufactured to correct for the anterior surface aberration of this eye.

Some manufacturers have attempted to introduce a constant level of spherical aberration at all lens powers that is equal in magnitude but opposite in sign to the population mean for human eyes. As we previously reported, in a comparison of some of the available designs, some lenses achieve this goal over the entire dioptric power range (Biomedics Premier by Cooper Vision), some over part of the dioptric power range (PureVision [Bausch & Lomb]) and others do not achieve their intended goal over any of the dioptric power range (Kollbaum and Bradley 2005). Lenses that we're aware of that have claimed to adopt this strategy include: Biomedics Premier (CooperVision), PureVision sphere and toric (B&L), Definition AC sphere and toric (Optical Connection) and Choice AB (CIBA Vision), which was recently discontinued.

Other strategies include developing contact lenses that have zero spherical aberration at all lens powers and, as such, will neither add to nor correct the eye's native spherical aberration. There are three potential advantages of this approach. First, such lenses with high power will not introduce the large amounts of spherical aberration contributed by standard spherical lenses. Second, as these lenses have no spherical aberration, they will not introduce coma as they decenter. Third, Artal, Chen et al (2003) have suggested that human vision is optimally adapted to the eye's own native aberration levels, and a correction that does not alter the levels of aberration may be optimal. More recent literature seems to contradict this notion, however (Chen, Artal et al, 2007). The only lens we're aware of that currently adopts this strategy is the Biomedics XC lens (CooperVision).

To date, however, none of these lenses have shown documented clinical success. However, with the wider availability of aberrometers, clinical studies will emerge that describe the eye's native aberrations as well as those while wearing the aberration-correcting lenses. Also, the newly available lens-only aberrometers (such as ClearWave by AMO-Wavefront Sciences) now make it possible for the research and manufacturing community to monitor the aberration characteristics of these aberration-correcting lenses. Therefore, we anticipate an increase in publications aimed at evaluating this exciting new technology, as well as in increase in the number of lenses being developed with goals of purposefully altering HOA in some meaningful way. CLS

To obtain references for this article, please visit http://www.clspectrum.com/references.asp and click on document #145.