The concept of scleral asymmetry was noted in 1977 when Bier and Lowther described scleral lens fitting issues such as the presence of air bubbles in the liquid reservoir behind the lens and conjunctival blanching; in their book, to overcome these issues, they recommended the use of spherical-oval fitting or toroidal shells with high scleral toricity.

More recent research on the ocular surface reported that scleral toricity was more pronounced in the scleral area than in the limbal area and that limbal and anterior scleral shapes were tangential rather than curved (van der Worp et al, 2010). With these findings, the researchers recommend the use of tangential angles rather than curves when fitting scleral lenses (van der Worp et al, 2010; van der Worp, 2010). Another study reported that the sclera presented a low toricity at a 15.0mm chord and that it increased in toricity further into the periphery. Therefore, it was suggested that scleral lens diameters of 14.5mm or less may be more rotationally symmetric, whereas diameters greater than 14.5mm may benefit from asymmetric designs (Ritzmann et al, 2016).

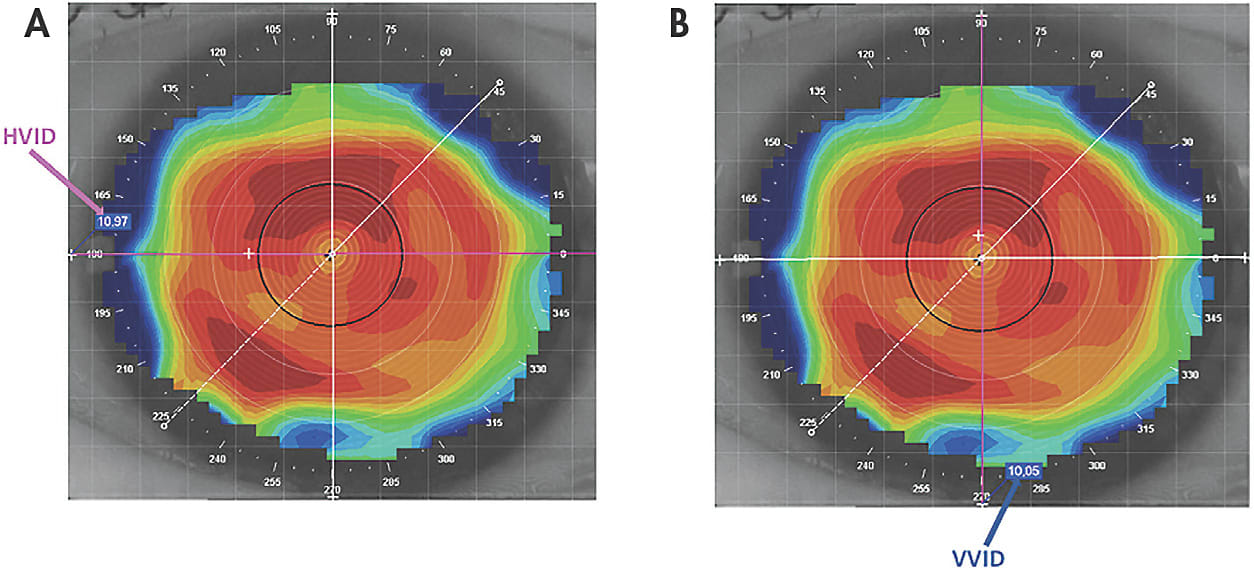
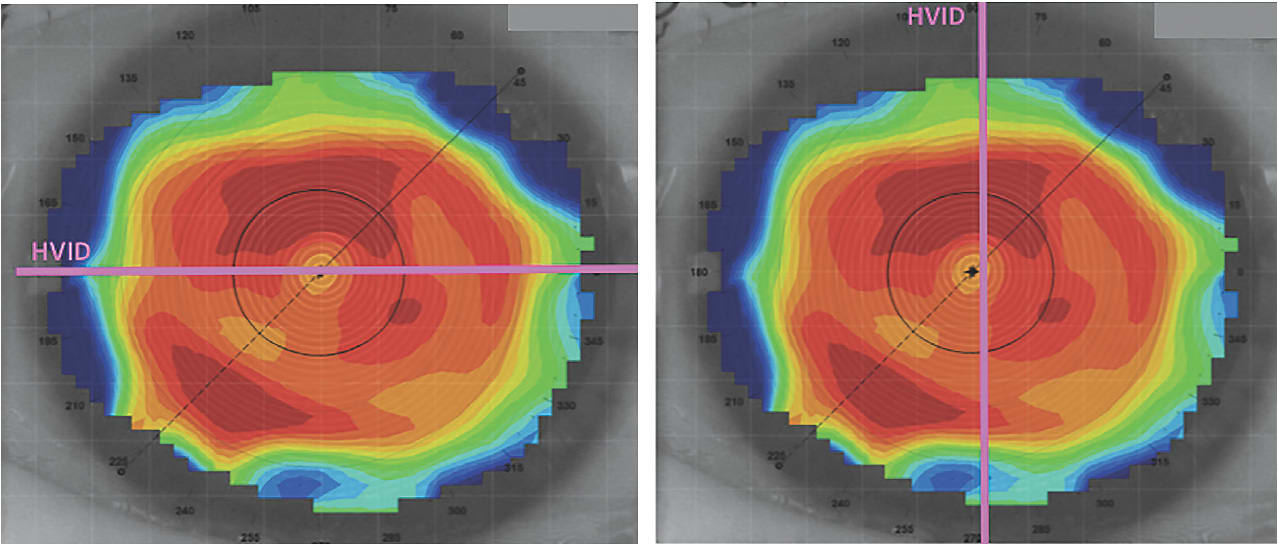
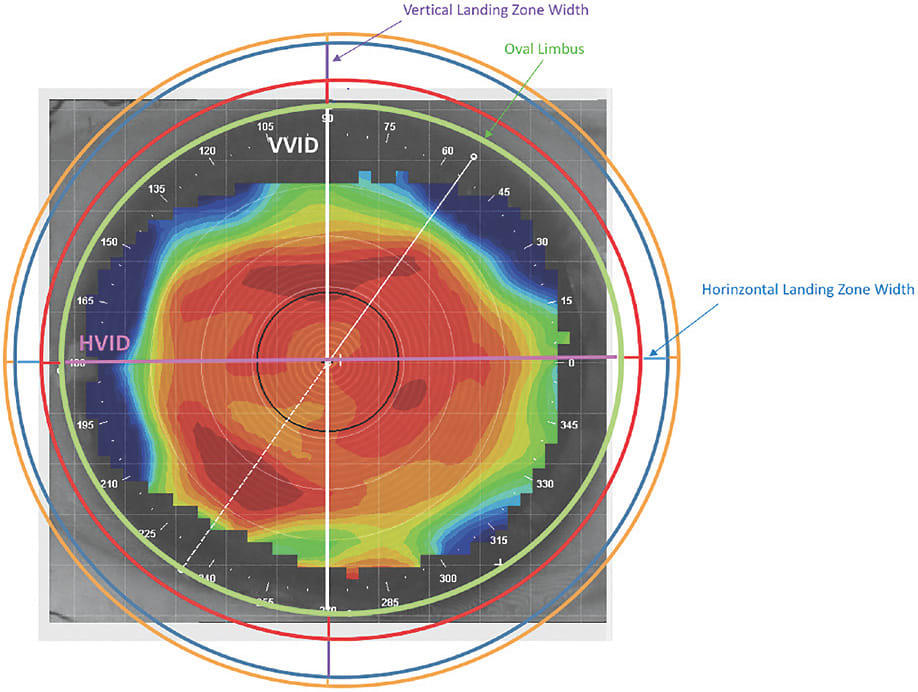
“Scleral toricity” is defined as the difference in height between the two principal meridians, while “scleral asymmetry” indicates that the height between meridians is not symmetric (Fadel, 2018). However, ocular surface toricity or asymmetry does not exist solely in the difference in height; it also pertains to diameter. This would include the limbus, which is not spherical but is more likely to have an oval shape. The horizontal visible iris diameter (HVID) is different and larger compared to the vertical visible iris diameter (VVID) (Figures 1 and 2). This is important data to take into consideration when fitting scleral lenses.

Symmetric Zone Diameters

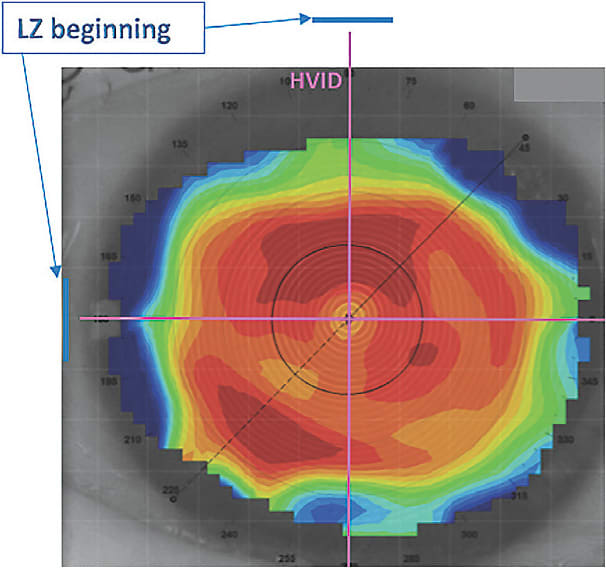
Scleral lens fitting is typically based on only the HVID value; this method may be valid in eyes with a more symmetrical limbus. The calculation of the total diameter of a scleral lens can be achieved by following this formula (Fadel, Aug. 2017):

(Note: limbal ZW is limbal zone width, LZW is landing zone width, and LPZW is the last peripheral zone width.)

Nevertheless, in some cases in which there is a substantial limbal oval shape, referring only to the HVID may result in a less-than-optimal fitting relationship in the vertical meridian, as the VVID may be significantly smaller. In fact, when fitting a round scleral lens and the limbus exhibits a significant oval shape, the lens will land near to the limbus in the horizontal meridian and will be positioned far from the limbus in the vertical meridian (Figure 3). This creates a greater clearance in the vertical axis, triggering negative pressure that results in debris entering into the fluid reservoir and in conjunctival prolapse. The excessive limbal clearance also may cause lens decentration, stem cell breakdown, corneal graft rejection, and discomfort (Fadel, May 2017; Fadel, Jun. 2017). Therefore, patients who have a limbus with a pronounced oval shape may benefit from an asymmetric lens with distinct diameters in the different meridians.

Fitting an Elliptic Scleral Lens

To achieve a better alignment with the limbal shape, the diameters of the internal zones of the scleral lens may be different in the two axes, 180° and 90° (Fadel, May 2017; Fadel, Jun. 2017). All of the internal lens zones (optical, limbal, landing, and last peripheral) may have different diameters in their two meridians (Figure 4). For this case, the diameters of the lens may be calculated following these formulas:

(Note: TD_H is the horizontal total diameter and TD_V is the vertical total diameter of the scleral lens.)

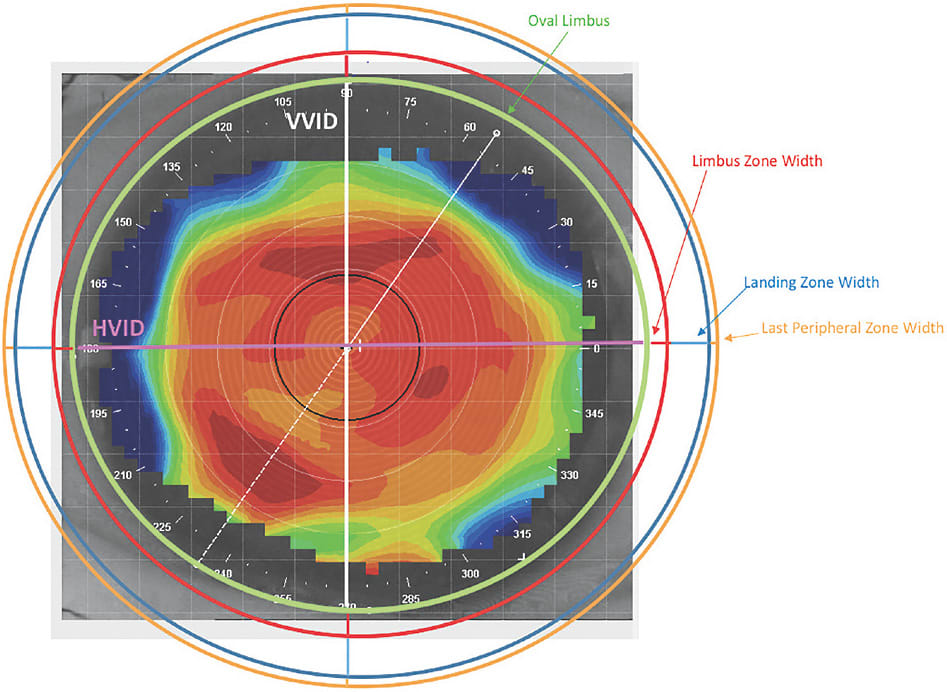
In this lens design, the visible iris diameter (VID) is the only diameter that differs in the two meridians; all outer diameters are equidistant. However, the different VID values lead to a different total lens diameter, which results in an elliptic shape; this also occurs with the limbus.

Fitting a Round Lens

Another design allowing a limbal fitting relationship may be obtained with a round lens that has the same total diameters in all quadrants. In this case, the landing zone compensates for the oval shape of the limbus (Figure 5). The calculation of the total diameter of this type of lens may be achieved via the use of these formulas:

(Note: LZDv is vertical landing zone diameter. It is calculated by determining the horizontal landing zone diameter [LZD_H]):

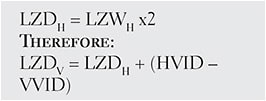
In this design, the limbal ZW and the LPZW have the same value in the two different meridians while the VID and LZD are different. The landing zone diameter compensates for the oval shape of the limbus, which results in a round lens. In both lens designs, an algorithm may be used to progressively calculate the lens diameter in each meridian.

Conclusions

Excessive limbal clearance can potentially result in lens decentration, conjunctival prolapse, stem cell breakdown, corneal graft rejection, and debris inflow in the tear reservoir. To manage these issues, practitioners can decrease the diameters of all internal zones.

In eyes in which the limbus has a pronounced oval shape, smaller diameters may solve the problems in the vertical meridian while potentially inducing limbal bearing in the horizontal one and causing potential stem cell breakdown. The stem cell failure is evident only in long-term wear. This situation may be acceptable in scleral lens fitting because the issues in the vertical meridian are visible in the short-term and, therefore, management may serve as a benefit. In fact, it may be undervalued.

Toric or asymmetrical scleral contact lenses with different diameters may be the best alternative for optimally fitting all meridians. Practitioners may be successful with two types of designs that may succeed: the first design may only have the VID different in the horizontal and vertical meridians, while all of the outside diameters remain equidistant; and the second design may have the VID and the landing zone with different values at 90° and 180°. Theses novel lenses will have the same limbal clearance in all meridians, which will result in optimal fitting and will provide better comfort. CLS

For references, please visit www.clspectrum.com/references and click on document #277.